Problems
- How much food to pack?
- How to carry what we pack?
- Shelter
- How to get there?
- What to do if you're lost?
- How to gather resources?
- Which knot to use?
- How to cross the river?
How Much Food?
The Problem: How much food should I bring on my camping trip?
![]() Activity! Food Calculator Create a "Camping Food Calculator" game - Design a calculator to estimate the needed food. Include: age, weight, height, activity level and trip duration.
Activity! Food Calculator Create a "Camping Food Calculator" game - Design a calculator to estimate the needed food. Include: age, weight, height, activity level and trip duration.
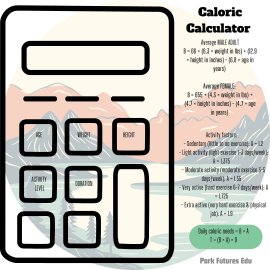
Calculate Daily Caloric Needs: Let's define variables:
- B = Base Metabolic Rate (BMR)
- A = Activity Factor
- D = Number of days camping
-
T = Total calories needed
Example Calculation: For a 30-year-old male, 170 lbs, 70 inches tall, camping for 3 days with moderate activity:
B = 66 + (6.3 × 170) + (12.9 × 70) - (6.8 × 30) = 1816 calories Daily needs = 1816 × 1.55 = 2815 calories T = 2815 × 3 = 8445 total calories
How Much to Carry?
The Problem: You have a backpack (knapsack) with a limited weight capacity, and you want to pack the most valuable supplies without going over that weight limit. You have a list of items, each with a weight and a value. You need to choose the best combination of items that fits within your backpack's weight limit while maximizing the total value of your packed items.
![]() Activity! Backpack Challenge Challenge child to "pack their backpack." If you can't get everything in the bag, ask child to empty it and pack it again.
Activity! Backpack Challenge Challenge child to "pack their backpack." If you can't get everything in the bag, ask child to empty it and pack it again.

Mathematic Approach -- Determine Food Weight: Let W be the total weight of food in pounds. Assuming an average of 125 calories per ounce of typical backpacking food:
W = (T ÷ 125) ÷ 16 (dividing by 16 to convert ounces to pounds)
The Algorithm's Approach:
The knapsack algorithm works like a clever decision maker for your packing. It considers all possible combinations of items and picks the one that offers the highest total value without exceeding the weight limit. In essence, the knapsack algorithm helps you make the most of your limited resources (backpack weight) by strategically selecting the items that offer the greatest value (most useful supplies for your hike).
(Imagine breaking down the problem) You start by considering the heaviest item. You can either take it or leave it. If you take it, you need to solve the same problem again, but with the remaining weight capacity and excluding that item. You do the same for leaving it out. Finally, you compare the best outcome from both scenarios (taking it or leaving it) and choose the one that gives you the most valuable backpack. This process continues for all items, ultimately revealing the optimal combination.
(Imagine building the solution step-by-step): Here, you methodically build the solution from the ground up. You create a table where each cell represents the maximum value achievable with a specific weight limit (considering all possible combinations of items up to that weight). By filling the table step-by-step, considering the value and weight of each item, you arrive at the final answer: the maximum value you can pack within your weight limit.
![]() Activity! What's In Your Bag?
Try this photo essay with your friends - take your bag, empty it and take a photo of everything inside. What does it say about you? What does their bag say about your friends? #whatsinmybag
Activity! What's In Your Bag?
Try this photo essay with your friends - take your bag, empty it and take a photo of everything inside. What does it say about you? What does their bag say about your friends? #whatsinmybag
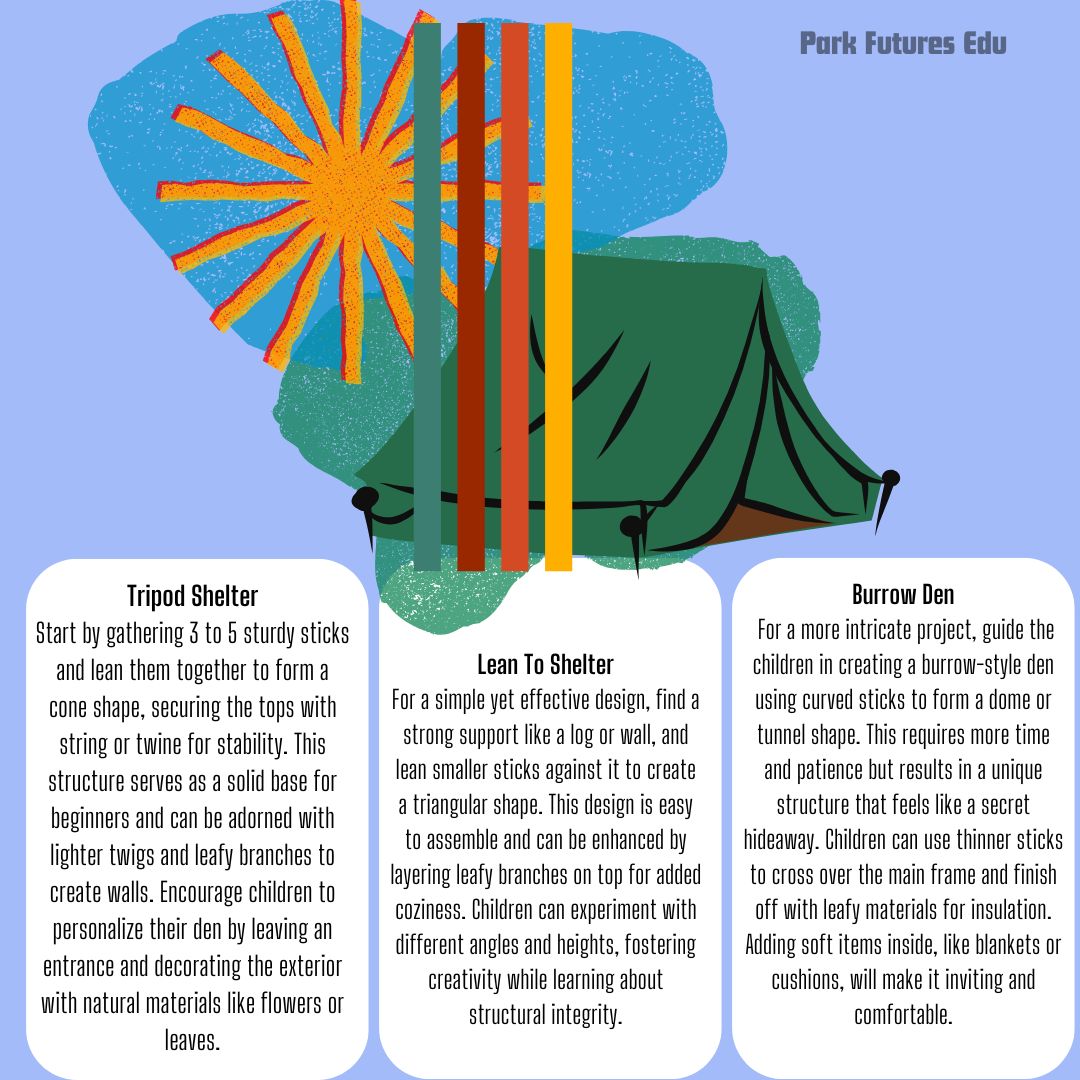
Shelter
![]() Activity! Build Your Own
Buying a tent is part of camping - try to find a used tent that is being given away or sold before committing to buying your own. While you are looking for a tent, try sleeping outside with shelter built by your own hands!
Choose a location: Find a sheltered area with a natural feature like a large rock or tree that can provide support for your shelter.
Activity! Build Your Own
Buying a tent is part of camping - try to find a used tent that is being given away or sold before committing to buying your own. While you are looking for a tent, try sleeping outside with shelter built by your own hands!
Choose a location: Find a sheltered area with a natural feature like a large rock or tree that can provide support for your shelter.
Collect enough branches and leaves to create a sturdy and weatherproof shelter. Lean the branches against the natural feature, creating a triangular shape. Use rocks or logs to secure the base of the branches. Place the leaves over the frame, creating a layer of protection from the elements. You may need to overlap the leaves to ensure complete coverage. Use additional branches or rocks to hold the leaves in place.

How to Get There?
The Problem: There are several points (landmarks, cities, sites etc) we want to get to, but what is the most efficient way?
Dijkstra's Algorithm is a powerful tool used to find the shortest path between two points in a weighted graph. Imagine you're planning a road trip and want to find the fastest route (shortest travel time) to your destination, considering traffic congestion on different roads. Dijkstra's Algorithm helps you navigate this efficiently.
We have a map represented as a weighted graph. Each location (city) is a node, and roads connecting them are edges. The weight on each edge represents the distance, travel time, or any other relevant factor you want to minimize. You define a starting point (your origin city) and a destination (your final destination).
![]() 2. Calculates a Tentative Distance
2. Calculates a Tentative Distance
The algorithm starts at the source node (your origin city) and considers all its neighboring nodes (cities connected by roads). For each neighbor, it calculates a tentative distance: the distance from the starting point to the current node (your origin to the neighboring city) plus the weight of the edge connecting them (travel time on the connecting road). Initially, these tentative distances are estimates, and the algorithm hasn't explored further yet.
"Unvisited" set: This includes all nodes that haven't been definitively explored yet (cities you haven't considered for the final route). "Visited" set: This includes nodes where the algorithm has already determined the shortest distance from the starting point (cities you've considered and their shortest travel times so far).
![]() 4. Calculates New Tentative Distance
4. Calculates New Tentative Distance
The algorithm repeatedly selects the node from the "unvisited" set with the current shortest tentative distance from the starting point (the closest unvisited city based on current estimates). Once a node is selected, it's moved to the "visited" set. Now, the algorithm considers all the unvisited neighbors of this newly visited node. For each neighbor, it calculates a new tentative distance: distance to the current node (previously visited city) plus the weight of the edge connecting them (travel time on the road connecting them). If this new tentative distance is shorter than the previously estimated distance for that neighbor, the algorithm updates the neighbor's tentative distance with the shorter value. This essentially refines the path possibilities as exploration progresses.
![]() 5. Identified the Shortest Distance
5. Identified the Shortest Distance
The algorithm continues this process of selecting the closest unvisited node, visiting it, and updating tentative distances for its neighbors until it reaches the destination node (your final destination city). By the time it reaches the destination, the algorithm has identified the shortest distance (fastest travel time) and can trace the path backward from the destination to the source node, revealing the optimal route.
It guarantees finding the shortest path for weighted graphs where all edge weights are non-negative (travel times are never negative). It's efficient for finding single-source shortest paths, meaning it focuses on finding the best route from a specific starting point to all other reachable destinations.
![]() Dijkstra's Algorithm applications
Dijkstra's Algorithm applications
GPS navigation systems: It helps determine the fastest route for drivers considering traffic conditions. Computer network routing: It helps route data packets across networks efficiently. Social network analysis: It can be used to find the shortest path of connections between users in a social network. Overall, Dijkstra's Algorithm is a powerful tool for navigating complex networks and finding the most efficient route between points, making it a valuable asset in various fields.
Lost?
How to Gather Resources?
The Problem: You need to collect fire wood. What is the most efficient way to get it all before sundown?
![]() Collecting wood - a math game -
Collecting wood - a math game -
Ask first person to collect one stick. Next to collect two. Next to collect 4 and keep doubling the number - or set up the students and ask each one to collect double the previous person.
<y = a * b^x > y is the final value / a is the initial value / b is the growth factor (1 + growth rate) / x is the time or number of periods
Knots
Taut-line Hitch
- Securing tent guy lines
- Adjusting tent rainfly tension
- Setting up tarps at campsites
- Scouting
- Wilderness survival skills
- Knot-tying badge requirements
- Setting up temporary shelters
- Building forts
- Creating hammock setups
- Hanging outdoor play equipment
- Making clotheslines
- Creating temporary shelters
- Hanging equipment while hiking
- Securing gear during outdoor expeditions
Figure 8 (Stopper knot)
Two Half Hitches
- Securing tent guy lines
- Hanging tarps
- Attaching ropes to trees or posts
- Setting up hammocks
- Hanging clotheslines
- Knot-tying badge requirements
- Securing equipment during camping trips
- Building forts
- Creating play structures
- Hanging lightweight equipment
- Creating temporary shelters
- Securing temporary shelters
- Securing hiking gear
- Tying down equipment during outdoor expeditions
- Hanging lightweight items
- Securing tarps for yard work
- Creating adjustable rope systems
- Hanging garden equipment
Two-half hitch vs taut-line hitch
Taut-line Hitch:
Adjustable tension: Use when you need to adjust the tension of a line frequently, such as with tent guy lines or tarp setups. Variable conditions: Ideal for situations where conditions may change, like mooring boats in areas with changing tide levels. Temporary setups: Good for temporary installations that require occasional tightening or loosening. Camping gear: Useful for hanging adjustable clotheslines or creating adjustable hangers for camping equipment.
Two Half Hitches:
Fixed attachment: Better when you need to secure a rope to a fixed object without the need for frequent adjustment. Quick and simple tie: When you need a reliable knot that's quick to tie and doesn't require adjustment. Heavier loads: Generally considered more secure for heavier loads compared to the taut-line hitch. Pioneering projects: Often used in Scout pioneering projects for securing guylines or large ropes. Hanging hammocks or clotheslines: When a fixed, secure attachment is needed between two points.
Fifth grade Ling's Hiking Trail Question